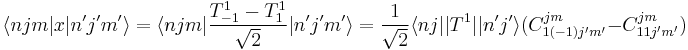Wigner–Eckart theorem
The Wigner–Eckart theorem is a theorem of representation theory and quantum mechanics. It states that matrix elements of spherical tensor operators on the basis of angular momentum eigenstates can be expressed as the product of two factors, one of which is independent of angular momentum orientation, and the other a Clebsch-Gordan coefficient. The name derives from physicists Eugene Wigner and Carl Eckart who developed the formalism as a link between the symmetry transformation groups of space (applied to the Schrödinger equations) and the laws of conservation of energy, momentum, and angular momentum.[1]
The Wigner-Eckart theorem reads:
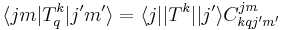
where 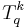 is a rank
is a rank 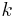 spherical tensor,
spherical tensor, 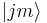 and
and 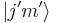 are eigenkets of total angular momentum
are eigenkets of total angular momentum 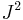 and its z-component
and its z-component 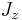 ,
, 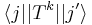 has a value which is independent of
has a value which is independent of 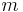 and
and 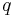 , and
, and 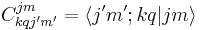 is the Clebsch-Gordan coefficient for adding
is the Clebsch-Gordan coefficient for adding 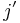 and
and 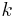 to get
to get 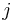 .
.
In effect, the Wigner–Eckart theorem says that operating with a spherical tensor operator of rank 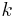 on an angular momentum eigenstate is like adding a state with angular momentum
on an angular momentum eigenstate is like adding a state with angular momentum 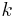 to the state. The matrix element one finds for the spherical tensor operator is proportional to a Clebsch-Gordan coefficient, which arises when considering adding two angular momenta.
to the state. The matrix element one finds for the spherical tensor operator is proportional to a Clebsch-Gordan coefficient, which arises when considering adding two angular momenta.
Example
Consider the position expectation value 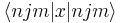 . This matrix element is the expectation value of a Cartesian operator in a spherically-symmetric hydrogen-atom-eigenstate basis, which is a nontrivial problem. However, using the Wigner–Eckart theorem simplifies the problem. (In fact, we could get the solution right away using parity, but we'll go a slightly longer way.)
. This matrix element is the expectation value of a Cartesian operator in a spherically-symmetric hydrogen-atom-eigenstate basis, which is a nontrivial problem. However, using the Wigner–Eckart theorem simplifies the problem. (In fact, we could get the solution right away using parity, but we'll go a slightly longer way.)
We know that 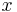 is one component of
is one component of 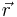 , which is a vector. Vectors are rank-1 tensors, so
, which is a vector. Vectors are rank-1 tensors, so 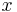 is some linear combination of
is some linear combination of 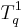 for
for 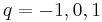 . In fact, it can be shown that
. In fact, it can be shown that 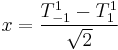 , where we defined the spherical tensors[2]
, where we defined the spherical tensors[2] 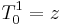 and
and 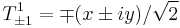 (the pre-factors have to be chosen according to the definition[3] of a spherical tensor of rank
(the pre-factors have to be chosen according to the definition[3] of a spherical tensor of rank  . Hence, the
. Hence, the 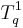 are only proportional to the ladder operators). Therefore
are only proportional to the ladder operators). Therefore
The above expression gives us the matrix element for  in the
in the 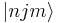 basis. To find the expectation value, we set
basis. To find the expectation value, we set 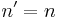 ,
,  , and
, and 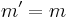 . The selection rule for
. The selection rule for 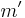 and
and  is
is 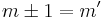 for the
for the 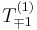 spherical tensors. As we have
spherical tensors. As we have 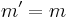 , this makes the Clebsch-Gordan Coefficients zero, leading to the expectation value to be equal to zero.
, this makes the Clebsch-Gordan Coefficients zero, leading to the expectation value to be equal to zero.
References
- ^ Eckart Biography– The National Academies Press
- ^ J. J. Sakurai: "Modern quantum mechanics" (Massachusetts, 1994, Addison-Wesley)
- ^ J. J. Sakurai: "Modern quantum mechanics" (Massachusetts, 1994, Addison-Wesley)
External links
- J. J. Sakurai, (1994). "Modern Quantum Mechanics", Addison Wesley, ISBN 0-201-53929-2.
- Weisstein, Eric W., "Wigner–Eckart theorem" from MathWorld.
- Wigner–Eckart theorem
- Tensor Operators